
“We look at this Son and see the God who cannot be seen. We look at this Son and see God’s original purpose in everything created. For everything, absolutely everything, above and below, visible and invisible, rank after rank after rank of angels—everything got started in him and finds its purpose in him. He was there before any of it came into existence and holds it all together right up to this moment. And when it comes to the church, he organizes and holds it together, like a head does a body.” (Colossians 1:15-18, The Message)
Paul says in Colossians that in Christ all things hold together. In Part One of this blog, I tried to explain an example of this in how the Fibonacci numbers are found in the natural world. Now in Part Two, I will try to do the same for the Golden Ratio, a ratio that is found both in the natural world and in arts created by human beings.
What is the Golden Ratio?
In Part One, we saw that the Fibonacci Sequence is a sequence of numbers that starts with 1 and 1 and in which the next number is obtained by adding the two previous ones. 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8 so the sequence is 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … and so on ad infinitum.
Before we go any further, I suggest that you stop reading at this point and view a 7:31 minute TED talk entitled ‘The (ab)surd golden ratio’ by Robb Enzmann‘ of Miami University.
I hope you found that informative and enjoyable. Now for more on how this ratio links with the Fibonacci numbers and how it occurs in the natural world.
The Golden Ratio and the Fibonacci numbers
As Professor Enzmann shows in the TED talk, as we go through the Fibonacci numbers dividing each one by the one before it, the answers converge on a number that begins 1.6180339887 …..
1/1 = 1, 2/1 = 2, 3/2 = 1.5, 5/3 = 1.666…, 8/5 = 1.6, 13/8 = 1.625, 21/13 = 1.61538…
This number is an irrational number like pi (π). In other words, it goes on for ever and cannot be expressed as a fraction for any whole numbers. (0.33333… goes on for ever but it can be expressed as 1/3.) The Golden Ratio is represented by the Greek letter phi (φ).
This can be presented visually by making a picture starting with two small squares of size 1×1 next to each other. On top of them, we can draw a 2×2 square. Beside them we can then draw a 3×3 square and below them a 5×5 square and so on for as long as we like.
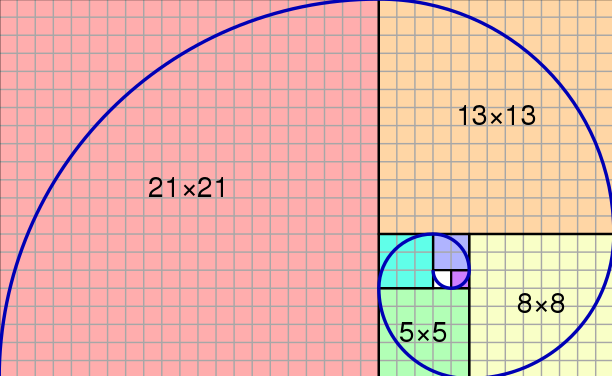
Each addition of a square makes the whole into a rectangle – 3×2, 5×3, 8×5, 13×8,… . As the process continues, the whole approximates more and more closely to a rectangle with sides in ratio 1.6180339887… to 1, i.e. a Golden Rectangle.
Golden Spirals in nature
The quarter circles shown above inside the squares form a spiral that approximates to what is known as the Golden Spiral or Phi Spiral.
This spiral often appears in the natural world. Examples include the shapes of sea shells and the shells of snails. The Nautilus sea shell is a frequently quoted and pictured example.
I have seen accounts which say this spiral is also seen in the shape of water spiralling down a drain, waves on the sea, hurricanes, and spiral galaxies. However, I notice that such examples are not usually mentioned by mathematicians so I am hesitant about saying that this is definitely the case. As Ian Stewart says, the literature can be “long on speculation but short on fact”.[1]
One undisputed example is in the case of the spirals we met in Part One – the spirals in seed heads and florets of composite flowers, e.g., the flower pictured at the top of this blog. The angle between primordial cells in the growth of the plant is crucial to the optimal packing of florets or seed heads and this angle is 137.5 degrees and is known as the Golden Angle. Only this angle leads to seeds with no overlaps or gaps. This is represented beautifully in Cristobal Vila’s ‘Nature by Numbers’ video (starting at 1:40 minutes).
At this point, I want to sing with Louis Armstrong (with tears in my eyes as he had in his!) ‘What a Wonderful World’!
The Golden Ratio in Architecture, Art, Music, …
The Golden Ratio has been known since the days of Pythagoras and Euclid. In his TED talk, Robb Enzmann says that it was known to the Mayans. It is therefore possible that it was known from early times by some architects, painters, sculptors, musicians and poets and deliberately incorporated in their work. On the other hand, there are many who hail the Golden Rectangle as the shape most pleasing to the eye and claim that it therefore is likely to occur naturally in artistic creations without deliberate and conscious intention.
The idea that the Golden Rectangle is the most pleasing shape is open to criticism. In his TED talk, Rob Erzmann quotes research done in the 19th century when people were given a group of rectangles and asked to pick their favourite one. The one he picks out on the screen as being most often chosen is not the Golden Rectangle. However, not knowing about any such research, I often gave this task to students when I was teaching Mathematics and I have to say they usually chose the Golden Rectangle! Perhaps they had read up about it in advance and just wanted to give the answer their teacher expected!
Closeness of approximations to phi is also an issue. Mathematicians tend to shudder when they see phi rounded down to 1.6 and claims made that Golden Rectangles are present on the basis of such rough approximations. They tend to be happier with the observation that the proportions of the credit card are very close to the Golden Ratio. Did it just happen that way … or was that ratio deliberately chosen?
Architecture: Golden Rectangles are claimed to exist in buildings as old as the Parthenon of Athens and the Great Pyramid of Giza. The approximations are reasonably good but there no documents to show whether this was intentional.
In modern times, the Swiss architect Le Corbusier and others have intentionally made use of the Golden Ratio in their designs.
The Core, the education building at Cornwall’s Eden Project, was inspired by the plant architecture of sunflower heads. Eden’s director of learning, Dr Jo Readman, says, “We wanted a building the shape of a sunflower and the size of a spaceship. Nature has a fundamental blueprint which goes beyond DNA. We have translated that blueprint into the structure of this amazing building.”
Painting and Sculpture: Close approximations to the Golden Rectangle may exist in the work of da Vinci, Michelangelo, Seurat and Mondrian. Some cubist and modern painters, e.g., Salvador Dali in his The Sacrament of the Lord’s Supper, have deliberately sought to use the Golden Rectangle in their work.
Ron Knott says that there are clearly Golden Ratios in Graham Sutherland’s huge tapestry of ‘Christ the King’ behind the altar in Coventry Cathedral.
Music: The Golden Ratio has also been claimed to exist in the compositions of Mozart, Beethoven, Bach, Schubert, Debussy and Bartók. Some modern composers have deliberately sought to use Fibonacci numbers in their work.
In an interesting video entitled ‘The Golden Ratio and Fibonacci Sequence in Music’, classical pianist Nahre Sol and drummer LA Buckner discuss what are called ‘Phi moments’. These occur when the climax of a piece of music occurs at a point in the whole that lands close to the Golden Ratio. Examples they give include ‘Under Pressure’ by Queen and David Bowie and ‘In My Feelings’ by Drake and they suggest that Phi moments occur naturally and these musicians weren’t “writing songs with calculators by their sides”.
What should we conclude from all this? It is clearly the case that many creative people find the Golden Rectangle to be a pleasing shape albeit not necessarily the most pleasing shape. Their art deliberately imitates nature and therefore reflects natural beauty. On the other hand, even though exaggerated claims are often made by the over-enthusiastic who see the Golden Ratio everywhere, it seems to me quite likely that human creativity should unconsciously and without deliberate intent manifest these beautiful proportions. They are clearly there in the natural world and most clearly in the plant kingdom so it is hardly surprising that they should be present in works of human creation. And I think to myself, what a wonderful world!
Let us pray
Creator God, we thank you for the wonderful and beautiful world you have made and for the beauty of so much architecture, paintings, sculptures, music, song, poetry that we human beings, made in your image, have made and do make. Help us to recognise and appreciate beauty wherever we find it and to discover and employ our own creative gifts. In Jesus’ name, Amen.
P.S. If you would like to be notified when new blogs are posted, please EITHER (1) email me through the contact address on this website OR (2) message me if you have come here via a link posted on Facebook.
[1] Ian Stewart, ‘Nature by Numbers’, The Times, 5 May 2011.
